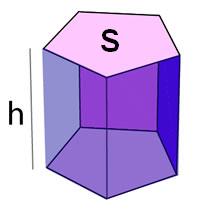
Prisma é um poliedro que tem como principal caracteristica dois lados paralelos e de medidas iguais e arestas principais paralelas que ligam os vertices das bases.
Oblico: se as arestas nao forem perpendiculares às bases.
Reto: se as arestas forem perpendiculares às bases.
PRISMA REGULAR
É o prisma que tem as arestas perpendiculares as bases e tem as bases regulares.
VOLUME DO PRISMA
Volume do prisma é o produto da area da base pela altura.
V= Sh
ÁREA DE UM PRISMA
Soma da area de todas as faces do prisma.
EXEMPLO:
(EUMT - LONDRINA) O volume de ar contido em um galpão com a forma e as dimensões dadas pela figura
abaixo é:
a) 300 b) 240 c) 225 d) 210 e) 180 |  |
RESOLUÇÃO
Calcula-se primeiro o volume do retangulo despresando a area do teto.
c: comprimento V'= C x L x h
l: largura V'= 10 x 6 x 3
h: altura V'= 180 m³
S: Área da base
V': volume prisma retangular
Agora calcule o volume do teto.
V''= b x h
h: altura do triangulo 2
bt: base do triangulo V''= 6 x 10 x 2
V'': volume prisma triangular 2
V''= 60 m³
agora calcular o volume total.
V': volume prisma retangular Vt= V' + V''
V'': volume prisma triangular Vt= 180 + 60
Vt: volume total do prisma. Vt= 240 m³
dando como resposta a letra "b".
Outra opção de resposta.
calcular a area da face e depois multiplicar pelo comprimento do prisma.
S: Area da face
C: comprimento do prisma
S= b*l + b*h S= 6 x 3 + 6 x 2 S= 24 m²
2 2
Vt= SC
Vt= 24 x 10
Vt= 240 m³
Fonte de pesquisa (livro.Coleção vestibular)
METODOS DE APLICAÇÃO EM SALA DE AULA
Esse é um breve resumo sobre prisma e fica a criterio do professor a forma de se trabalhar essa figura, porem o metodo mais aconselhavel é com a inclusao digital que facilita o aprendizado do aluno.
ESPERO QUE ESTE BLOG TENHA LHES TIRADO ALGUMAS DUVIDAS.
